С. Кузьмичёв, А. Хализов aka Haliz
Земля имеет форму чемодана, или Как сделать глобус чего угодно.
 Давным-давно, года три с половиной назад, мы продавали карты родного города. Карта была большой, по тем временам, и очень подробной. Чтобы продажа шла быстрее, решили дать объявление в газету. В процессе работы над текстом обратились к теме старых анекдотов, в общем в объявлении прошла такая фраза: «Глобус города Тольятти». И что вы думаете, пришлось таки одному потенциальному клиенту объяснять, что это была такая шутка, что имелась в виду карта и что такие глобусы бывают только в анекдотах. Он расстроился. Тут бы и конец истории, да вот в чью-то светлую голову пришла блестящая мысль о том, что если всё таки изловчиться и сделать глобус города, то веселее шутки не придумать. И то правда, вот что подарить на день рождения человеку у которого всё есть? А как насчет глобуса города? Стопроцентный результат! Решили мы заняться этим вопросом. Не все правда верили в успех этого безнадёжного дела, но время нас рассудило. Давным-давно, года три с половиной назад, мы продавали карты родного города. Карта была большой, по тем временам, и очень подробной. Чтобы продажа шла быстрее, решили дать объявление в газету. В процессе работы над текстом обратились к теме старых анекдотов, в общем в объявлении прошла такая фраза: «Глобус города Тольятти». И что вы думаете, пришлось таки одному потенциальному клиенту объяснять, что это была такая шутка, что имелась в виду карта и что такие глобусы бывают только в анекдотах. Он расстроился. Тут бы и конец истории, да вот в чью-то светлую голову пришла блестящая мысль о том, что если всё таки изловчиться и сделать глобус города, то веселее шутки не придумать. И то правда, вот что подарить на день рождения человеку у которого всё есть? А как насчет глобуса города? Стопроцентный результат! Решили мы заняться этим вопросом. Не все правда верили в успех этого безнадёжного дела, но время нас рассудило.
Сначала вспомнили, что раньше глобусы клеились из «лепестков». Нашли старый глобус. Удостоверились, что задача в принципе проста и выполнима. Правда как потом выяснилось – простой она казалась только на первый взгляд. Вспомнили про развёртку глобуса, о которой повествовал школьный учебник географии, и занялись её расчетами. Для этого пришлось проштудировать заново школьный курс геометрии и начертательной геометрии первого курса института. Для тех кто захочет повторить наш путь посоветуем учебники «Геометрия» (школьный курс), «Начертательная геометрия» раздел «Условные развёртки неразвертывающихся поверхностей»1 . Ну а для тех кому не охота сильно ломать голову, собственно и предназначено наше дальнейшее описание. Мы постарались как можно меньше давать различных формул, частных случаев и выводов, которыми изобилуют учебники, но совсем без них обойтись не удалось. Также на приведенных ниже рисунках мы в графическом виде постарались изобразить результаты вычислений. Надеемся, что всем все будет понятно.
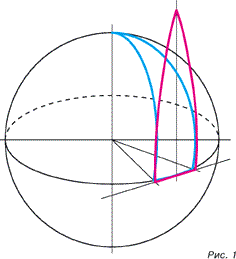
Итак, начинаем разворачивать «лепесток» на плоскость (рис. 1)2.
Глядя на рис. 2б выясняем что нам надо узнать для начала ширину основания – AB. Это ничто иное как дуга экватора. В нашем случае мы поделили экватор на 12 частей (рис. 2в).
Отсюда 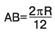 , где R – радиус шара (ОC на рис. 2а). , где R – радиус шара (ОC на рис. 2а).
Вычисляем длину CC6. Так как участок меридиана от экватора до полюса есть четверть длины окружности (экватора), то CC6 = 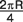 . .
Следующий шаг – нам нужно выяснить длины отрезков А1В1,...,А5В5 и их положение в плане.
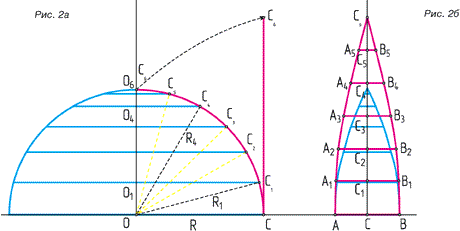
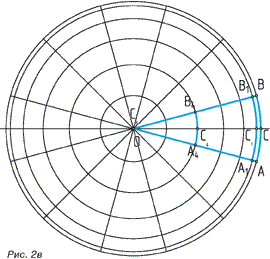 В общем случае В общем случае 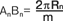 , ,
где m – количество секторов поделённого на равные части экватора.
Единственная неизвестная величина Rn – которая по сути является радиусом окружности параллельной экватору (параллель) и проходящей через точки Аn, Bn, Сn.
Радиусы параллелей вычисляются следующим образом. Получим дополнительные точки C1,...,C5. Поделим прямой угол C6ОC в приведенном случае на шесть равных частей (рис. 2а). Получим пять дополнительных отрезков C1О,...,C5О. Широты полученных точек будут отличаться друг от друга приращением в 15о (90о/6). Исходя из того факта, что отрезки C1О,...,C5О равны между собой и являются радиусами R нашего глобуса, то собственно говоря через этот известный радиус и находятся все остальные радиусы параллелей. Глядя на рис. 2а видим, что треугольник C1ОО1 – прямоугольный. Из школьной программы нам известно, что в данном случае О1C1=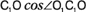 , угол этот равен углу C1ОC1. , угол этот равен углу C1ОC1.
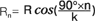 , где k – количество секторов поделённой на равные части четверти меридиана.
Для нашего случая в 6 секторов – R1= R cos15о, R2= R cos30о и т. д. Проверяя себя берем экстремумы функции: n=0 -> Rn=R (радиус экватора) и n=m -> Rn=0 (радиус полюса)3. , где k – количество секторов поделённой на равные части четверти меридиана.
Для нашего случая в 6 секторов – R1= R cos15о, R2= R cos30о и т. д. Проверяя себя берем экстремумы функции: n=0 -> Rn=R (радиус экватора) и n=m -> Rn=0 (радиус полюса)3.
Итак мы нашли способ вычислить радиус любой параллели и вместе с этим вычисления длины дуги для любой параллели.
Собственно говоря первый этап нахождения формул мы на этом закончили и можем приступить к вычислениям нужных значения.
Что имеем:
(i) Длина основания 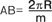 , где m – количество секторов поделённого на равные части экватора. , где m – количество секторов поделённого на равные части экватора.
Частный случай более общей формулы (iii).
(ii) Длина искомой части дуги меридиана СС6= 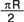 . .
(iii) Длина искомой части дуги заданной параллели АnBn=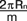 , где m – количество секторов поделённого на равные части экватора, , где m – количество секторов поделённого на равные части экватора,
(iiii) а Rn вычисляется по формуле Rn=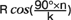 , где k – количество секторов поделённой на равные части четверти меридиана. , где k – количество секторов поделённой на равные части четверти меридиана.
Исходя из того, что С1С2=С2С3=...=С5С6 – длины дуг поделённого на равные части сектора СОС6 получаем
С(n-1)Cn=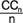 . .
 Длины дуг AnBn мы после этого делим пополам. Как видно из рисунка 2б точки Аn и Bn располагаются симметрично относительно оси СС6. Длины дуг AnBn мы после этого делим пополам. Как видно из рисунка 2б точки Аn и Bn располагаются симметрично относительно оси СС6.
Составив небольшую программку на любом удобном вам языке программирования или проделав все вычисления на калькуляторе мы получаем таблицу координат точек В,...,Вn.
Сразу могу сказать, что для стандартного глобуса Уральской фабрики диаметром 210 мм, путём многочисленных проб были найдени достаточни оптимальные числа: экватор делили на 18 частей, меридиан на 30 частей. Меньше – бумагу начинало «морщить», больше – скажем так, слишком большой объем ручных действий, при практически том же качестве конечного результата. Извиняемся за небольшое отступление. Продолжаем дальше.
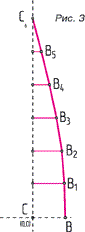
В вашем векторном редакторе5 строите кривую по координатам получившися точек.(рис. 3) Затем делаете копию, «зеркалите» её относительно СС6 (кстати точка С в даннных вычислениях является центром начала координат, надеюсь вы об этом не забыли и перенесли ЦНК в точку С). Соединяете получившиеся две кривые в единое целое и сделав копию получившейся фигуры, «зеркалите» её заново, теперь уже относительно АВ. Соединяете в единое целое.
ВУАЛЯ!!! Получился «лепесток»
(см. рис. 4).
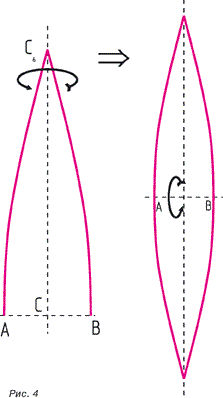
Теперь можно было бы и сдублицировать все лепестки, но мы бы не советовали вам делать на данном этапе.
И вот почему. Посмотрим еще раз на рисунок 2б. Дуга СС6 явно не равна дугам АС6 и ВС6, хотя тоже является меридианом, т.е. они должны быть равны по длине. Мы в свое время обратили внимание на этот факт, но не придали ему большого значения. На стадии сборки макета, у нас все склеилось в шар, хотя несколько удивил факт некоторого выгибания отрезка АВ вверх в результате чего средняя точка С оказывалась несколько выше (в районе 1 мм) крайних точек А и В.
Мы поделили план города6 на 540 (30*18) прямоугольных кусочков искривили их по получившимся частям лепестка, распечатали и акуратненько наклеили. То что мы увидели повергло нас, мягко выражаясь, в некоторую задумчивчивость и уныние.
На рисунке 5 мы схематично изобразили получившися результат. Если посмотреть сверху на глобус (со стороны полюса), то видно что вместо плавных параллелей получались 18-угольники, если посмотреть сбоку на то же самое «чудо», то как видно на том же рисунке параллели приняли вид «паучьей сетки». Все это в равной степени относилось и к остальным более-менее протяженным обектам, присутствующим на глобусе.
Но не бросать же на полпути такую хорошую шутку. Мы опять взялись за умные книги. И нашли ответ в учебнике «Начертательная геометрия». Опуская многословную теорию, начнем описание второй части наших расчётов.
Суть состоит в том, что поверхность вращения (в нашем случае – шар) может быть представлена множеством вписанных или описанных усечённых конусов. В нашем случае мы выбираем множество усечённых конусов вписанных в сферу и опирающихся своими основаниями на уже ранее найденные нами параллели.(рис. 6) 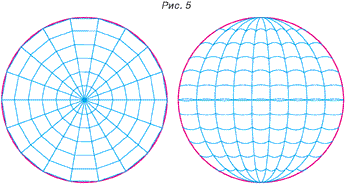
Внимательно посмотрев на рисунок 6 мы видим, что нам «жизненно необходимо» для дальнейшего продвижения нашего проекта знать координаты воображаемых вершин усечённых конусов. 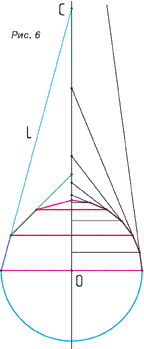 Попробуем решить эту задачу. Попробуем решить эту задачу.
Из рисунка 7 видно, что к вершине С нас приводит образующая L. Которую, опять же, опуская ненужную в данный момент теорию, мы найдем из такого простого выражения:
L(n-1)=AC=. 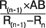
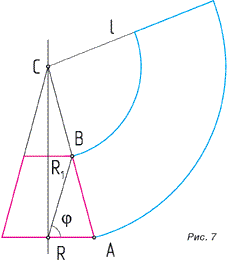
Разберём на части наше выражение и выясним что нам известно, а что – нет. R(n-1) – радиус параллели, которая собственно и является основанием усечённого конуса, Rn – радиус следующей параллели, которая будет представлять собой верхнее основание того же усечённого конуса. Эти величины мы вычислили на первом этапе. Осталось найти длину АВ. АВ вычисляется по формуле:
AB=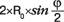 где R0 – радиус глобуса, j – приращение (шаг) широты. АВ – величина постоянная для всех наших усечённых конусов и вычисляется один раз.
где R0 – радиус глобуса, j – приращение (шаг) широты. АВ – величина постоянная для всех наших усечённых конусов и вычисляется один раз.
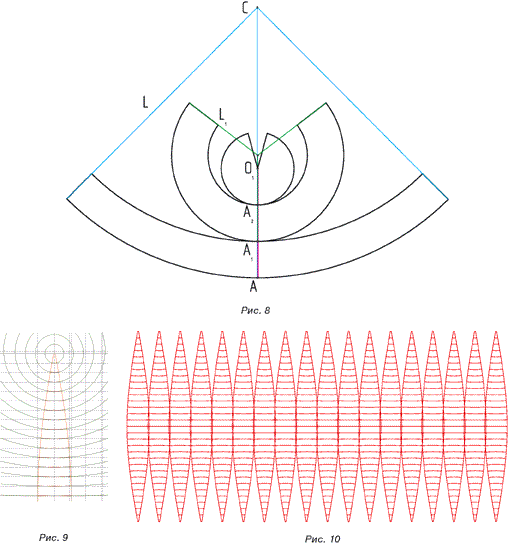
На рисунке 8 мы показали как выглядят развертки трёх усечённых конусов, которые при свёртке будут составлять половину глобуса. Но нам требуется совместить развёртку глобуса полученного первым способом, где учитываются искажения по горизонтали, с развёрткой полученной вторым способом, где учитываются искажения по вертикали. Делается это следующим образом.
Берём половину полученного ранее «лепестка» («северную» или «южную» не имеет значения). Строим «массив» окружностей, где радиусы равны соответсвующим образующим. Центры окружностей лежат на вертикальной оси симметрии «лепестка».
Получается примерно такая картина изображенная на рисунке 9. Для получение перекрытия мы раздали лепесток «в ширь» на 1 мм. В векторных пакетах это делается легко – операция типа Offset Path в Adobe Illustrator или Contour в CorelDraw.Теперь можно «порезать» лепесток на части этими получившимися окружностями. Далее простые операции копирования и дублицирования приводят нас к виду представленному на рисунке 10.
Распечатали, вырезали и наклеили (тщательно и осторожно) получившуюся развертку на глобус. Обнаруживаем, что у нас все линии на своих местах: параллели ровные и параллельны экватору, меридианы ровные и перпендикулярны экватору.
Далее персонально для одного из авторов данной статьи начался «личный ад». :) Ему предстояло искривить прямоугольные блоки порезаной картографичекой основы в соответствии с получившимися «трапециями» (кстати не забудьте при резке основы на прямоугольники сделать перекрытие – по 1 мм справа и слева, сверху и снизу этого делать не надо). Операция Envelope присутсвующая в пакете CorelDraw с успехом автоматически «впихивала» прямоугольник в соответствующую трапецию, но при этом искривляла внутренние объекты «по-своему». Так что пришлось переключаться в ручной режим и проводить Envelope вручную. На рисунке 11(а, б) показана начальная и конечная фаза этого процесса.

Некоторые пояснения по ходу. Боковые средние точки можно удалить и боковые линии перевести из Curve в Line. Средние точки верхней и нижней кривой должны находиться в соответсвующих пересечениях осевой guideline c верхней и нижней ограничивающими guidelines, эти точки должны иметь тип Symmetrical. «Усики» этих точек должны лежать на соответствующих верхней и нижней ограничивающих guidelines. Угловые точки перемещаются в соответствующие точки шаблона-трапеции. Кривые выравниваются по шаблону-трапеции. Главное - точность подгонки.
И так 540 прямоугольничков. Достаточно нудная работа для дизайнера. :) Причем, заметьте, эту работу пришлось проделать 3 раза с самого начала, пока не получилась нормальная развёртка удовлетворяющая нашим требованиям. Если кто-нибудь подскажет нормальный способ автоматизации этого «узкого места» – будем признательны.
 Хорошо, что всё хорошо кончается. Развёртка готова. Печатаем мы её на цветном лазерном принтере. «Почему не струйном?» – спросите вы. Отвечаем. В процессе изготовления «лепестки» перед наклейкой на шар помещаются в воду на минутку другую. После такой процедуры они более ровно и плотно накладываются на глобус. Для приклеивания используется клей ПВА, который при высыхании становиться бесцветным и не ведёт бумагу. Т.к. бумага мокрая, то это дает дополнительное время для выравнивания «лепестков» относительно друг-друга и глобуса. Самое главное правильно приклеить первый «лепесток» (как можно ровнее по направлению меридиана), иначе погрешности при приклеивании имеют свойство накапливаться и «вылазить боком» в самом видном месте. :) Хорошо, что всё хорошо кончается. Развёртка готова. Печатаем мы её на цветном лазерном принтере. «Почему не струйном?» – спросите вы. Отвечаем. В процессе изготовления «лепестки» перед наклейкой на шар помещаются в воду на минутку другую. После такой процедуры они более ровно и плотно накладываются на глобус. Для приклеивания используется клей ПВА, который при высыхании становиться бесцветным и не ведёт бумагу. Т.к. бумага мокрая, то это дает дополнительное время для выравнивания «лепестков» относительно друг-друга и глобуса. Самое главное правильно приклеить первый «лепесток» (как можно ровнее по направлению меридиана), иначе погрешности при приклеивании имеют свойство накапливаться и «вылазить боком» в самом видном месте. :)
Последние советы:
– соотношение длины к высоте основы – 2:1 (половина длины экватора = длина дуги от полюса до полюса)
– высокие широты северного и южного полушарий подвергаются достаточно большим деформациям, верхний и нижний обрезы основы будут представлять собой соответственно Северный и Южный полюса. Так что еще раз проверьте и подумайте «куда ведут ваши дороги» :)
– левый и правый край вашей основы по сути один и тот же меридиан, здесь тоже надо все хорошенько «подогнать».
Совет последний: хорошенько потренируйтесь наклеивая развёртку без рисунка, скорее всего вам потребуется на несколько миллиметров изменить размеры развёртки в сторону увеличения или уменьшения. Все зависит от используемой бумаги. Бумага тоже тянется, причем в разных направлениях по разному.
То, что получилось у нас вы можете увидеть на фотографиии.
Еще раз задайтесь вопросом: «Много ли людей могут похвастаться тем, что у них на столе стоит глобус родного города (страны, квартала, дачного участка, квартиры, сортира)?» и «Стоит ли овчинка выделки?» :)
Удачных вам приколов!
[1] Поверхность шара, оказывается относится именно к этому типу поверхностей
[2] Для наглядности на рисунках некоторые пропорции и размеры искажены
[3]Нсе та же школьная программа, теорема «О перекрёстных углах в двух параллельных прямых пересекаемых третьей прямой» – за точность названия данной теоремы не ручаюсь, если кому охота выяснить точное название поройтесь в учебнике геометрии потому как здесь это не столь важно :)
[4] Вроде все правильно :) Уф! В уме представлять это гораздо проще, чем выписывать буковки и формулы. Теперь я понимаю почему я так не любил в школе доказывать теоремы у доски, руки не поспевают за мыслью :)
[5] Надеемся у Вас есть векторный редактор :), если нет то результаты можно вычертить на куске ватмана.
[6] особая благодарность ОАО «СамараТИСИЗ» за предоставленную картографичекую основу
P.S. Статья окончена 1 апреля 2002 года. Бывают же совпадения :)
P.P.S. По всем возникшим вопросам обращаться e-mail:haliz@mail.ru
P.P.P.S. Особая благодарность людям которые говорили нам: «Бросьте ребята это дело, ничего у вас не получиться». Если бы не они, мы бы действительно бросили. :)
Авторы: С. Кузьмичёв,
А. Хализов aka Haliz.
Дата размещения: 2002-04-08 11:18:36
|



